Neutron or X-ray scattering static structure factor S(q) is defined as:
where bj et
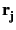 represent respectively the neutron or X-ray scattering length, and the position of the atom j.
N is the total number of atoms in the system studied.
represent respectively the neutron or X-ray scattering length, and the position of the atom j.
N is the total number of atoms in the system studied.
To take into account the inherent/volume averaging of scattering experiments it is necessary to sum all possible orientations of the wave vector q compared to the vector
 -
-  .
This average on the orientations of the q vector leads to the famous Debye's equation:
.
This average on the orientations of the q vector leads to the famous Debye's equation:
Nevertheless the instantaneous individual atomic contributions introduced by this equation [Eq. 5.7] are not easy to interpret.
It is more interesting to express these contributions using the formalism of radial distribution functions [Sec. 5.2].
In order to achieve this goal it is first necessary to split the self-atomic contribution (j = k), from the contribution between distinct atoms:
S(q) = 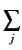 cjbj2 + cjbj2 + 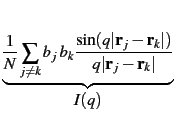 |
(5.8) |
with
cj = 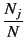 .
.
4π 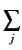 cjbj2 represents the total scattering cross section of the material.
cjbj2 represents the total scattering cross section of the material.
The function I(q) which describes the interaction between distinct atoms is related to the radial distribution functions through a Fourier transformation:
I(q) = 4πρ 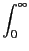 dr r2 dr r2 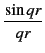 G(r) G(r) |
(5.9) |
where the function G(r) is defined using the partial radial distribution functions [Eq. 5.4]:
G(r) = 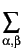 cαbα cβbβ (gαβ(r) - 1) cαbα cβbβ (gαβ(r) - 1) |
(5.10) |
where
cα = 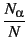 and
bα represents the neutron or X-ray scattering length of species α.
and
bα represents the neutron or X-ray scattering length of species α.
G(r) approaches -
- 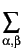 cαbα cβbβ for r = 0, and 0 for
r→∞.
cαbα cβbβ for r = 0, and 0 for
r→∞.
Usually the self-contributions are substracted from equation [Eq. 5.8] and the structure factor is normalized using the relation:
S(q) - 1 = 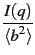 avec 〈b2〉 = avec 〈b2〉 = 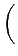 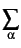 cαbα cαbα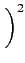 |
(5.11) |
It is therefore possible to write the structure factor [Eq. 5.7] in a more standard way:
S(q) = 1 + 4πρ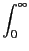 dr r2 dr r2 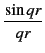 ( ( (r) - 1) (r) - 1) |
(5.12) |
where
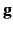 (r) (the radial distribution function) is defined as:
(r) (the radial distribution function) is defined as:
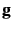 (r) = (r) = 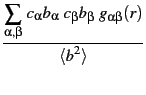 |
(5.13) |
In the case of a single atomic species system the normalization allows to obtain values of S(q) and
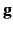 (r) which are independent of the scattering factor/length and therefore independent of the measurement technique. In most cases, however, the total S(q) and
(r) which are independent of the scattering factor/length and therefore independent of the measurement technique. In most cases, however, the total S(q) and
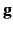 (r) are combinations of the partial functions weighted using the scattering factor and therefore depend on the measurement technique (Neutron, X-rays ...) used or simulated.
(r) are combinations of the partial functions weighted using the scattering factor and therefore depend on the measurement technique (Neutron, X-rays ...) used or simulated.
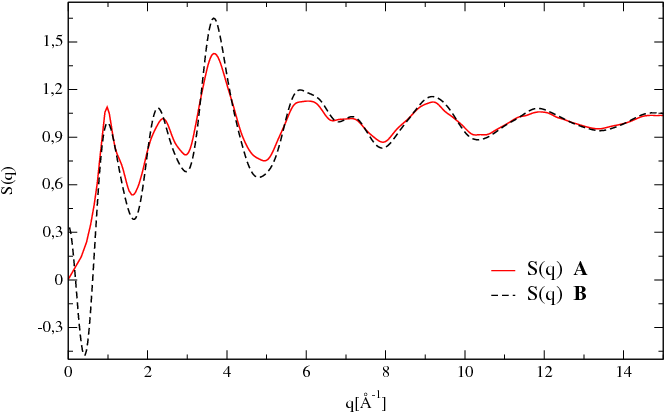
Figure 5.4:
Total neutron structure factor for glassy GeS2 at 300 K - A Evaluation using the atomic correlations [Eq. 5.7], B Evaluation using the pair correlation functions [Eq. 5.12].
|
|
Figure [Fig. 5.4] presents a comparison bewteen the calculations of the total neutron structure factor done using the Debye relation [Eq. 5.7] and the pair correlation functions [Eq. 5.12]. The material studied is a sample of glassy GeS2 at 300 K obtained using ab-initio molecular dynamics.
In several cases the structure factor S(q) and the radial distribution function
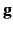 (r) [Eq. 5.13] can be compared to experimental data.
To simplify the comparison I.S.A.A.C.S. computes several radial distribution funcrions used in practice suh as G(r) defined [Eq. 5.10], the differential correlation function D(r),
(r) [Eq. 5.13] can be compared to experimental data.
To simplify the comparison I.S.A.A.C.S. computes several radial distribution funcrions used in practice suh as G(r) defined [Eq. 5.10], the differential correlation function D(r),
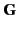 (r), and the total correlation function T(r) defined by:
(r), and the total correlation function T(r) defined by:
| D(r) = 4πrρ G(r) |
|
|
(5.14) |
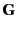 (r) = (r) = 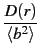 |
|
|
|
| T(r) = D(r) + 4πrρ 〈b2〉 |
|
|
|
 (r) equals zero for r = 0 and approaches 1 for
r→∞.
(r) equals zero for r = 0 and approaches 1 for
r→∞.
D(r) equals zero for r = 0 and approaches 0 for
r→∞.
 (r) equals zero for r = 0 and approaches 0 for
r→∞.
(r) equals zero for r = 0 and approaches 0 for
r→∞.
T(r) equals zero for r = 0 and approaches ∞ for
r→∞.
This set of functions for a model of GeS2 glass (at 300 K) obtained using ab-intio molecular dynamics is presented in figure [Fig. 5.5].
Figure 5.5:
Exemple of various distribution functions neutron-weighted in glassy GeS2 at 300 K.
|
|
I.S.A.A.C.S. can compute, for the case of x-ray or neutrons, the following functions:
- •
- S(q) and
Q(q) = q[S(q) - 1.0] [9,10] computed using the Debye equation
- •
- S(q) and
Q(q) = q[S(q) - 1.0] [9,10] computed using the Fourier transform of the
 (r)
(r)
- •
-
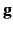 (r) and
(r) and
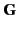 (r) computed using the standard real space calculation
(r) computed using the standard real space calculation
- •
-
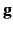 (r) and
(r) and
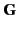 (r) computed using the Fourier transform of the structure factor calculated using the Debye equation
(r) computed using the Fourier transform of the structure factor calculated using the Debye equation
Sébastien Le Roux
2011-02-26