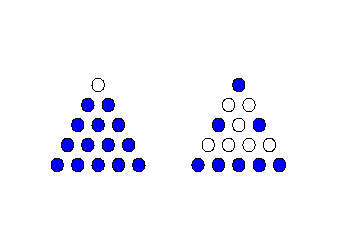
This problem was suggested by Chris Porter, a student at the Alma lecture.
Chris suggested doing the Genius problem in the following manner. It turns out that this is impossible.

Consider the Anti-Problem:
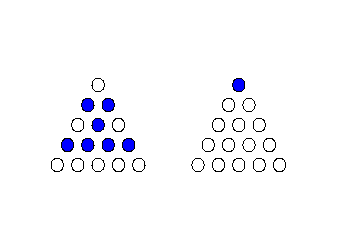
It is easy to see that the anti-problem is impossible by counting corner pegs.
(Corner pegs = e1, c3, a5, e5, i5, or g3. See Slide 12.)
The start position has no corner pegs. The finish position has 1 corner peg.
However, no jump can increase the number of corner pegs. Therefore, the problem is impossible.
Using the resource count on slide 25, you can also show that it is impossible to go from the starting position on the right to one hole in b4 or h4.
| Previous slide | Back to first slide | Back to index |