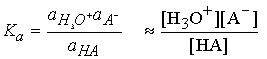Chapter 9 Chemical Equilibrium
Chemical reactions move toward a dynamic equilibrium in which both
reactants and products are present but don’t undergo net change. The direction of 'spontaneous' change is
toward lower values of Gibbs energy, G.
9.1 The Gibbs energy minimum
We locate the equilibrium composition of a reaction mixture by
calculating the Gibbs energy of the reaction mixture and identifying the
composition that corresponds to minimum G.
(a) The reaction Gibbs energy
Let's consider ![]() . Suppose an
infinitesimal amount, dx, of A turns into
B, Then the change in the amount of A present is dnA = -dx
and the change in the amount of B present is dnB = +dx
. Suppose an
infinitesimal amount, dx, of A turns into
B, Then the change in the amount of A present is dnA = -dx
and the change in the amount of B present is dnB = +dx
The quantity x is called the extent of reaction; it
has the dimensions of amount of substance and is reported in moles. When the extent of reaction changes by a
finite amount Dx, the amount of A present changes from nA
to nA,0 - Dx
and the amount of B changes from
nB to nB,0 + Dx.
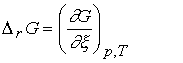
The reaction
Gibbs energy, DrG,
is
defined as the slope of the graph of Gibbs energy plotted against the extent of
reaction:
Usually, D signifies a difference, but in this case
Dr signifies a derivative, the slope of G with respect to x.
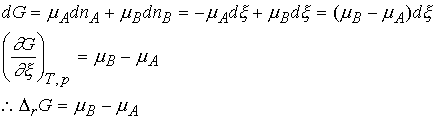
Thus DrG can be interpreted as the difference between chemical potentials of the reactants and products at the composition of the reaction mixture.
Because the chemical potentials vary with composition, the slope
of G against extent of reaction changes also.
For A Û B, the reaction
is spontaneous when mA > mB.
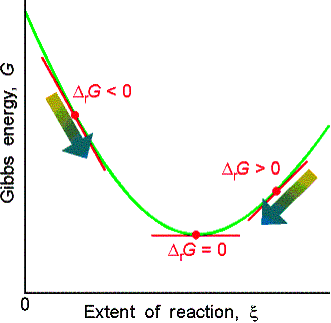

The slope is zero and the reaction is spontaneous in neither direction when DrG = 0.
(b) Exergonic and endergonic reactions
If DrG < 0, the
forward reaction is spontaneous. exergonic
If DrG > 0, the reverse reaction is spontaneous. endergonic
If DrG = 0, the reaction is at equilibrium. (neither exer- or
endergonic)
(c) Perfect gas equilibria
When A and B are perfect gases we can write,
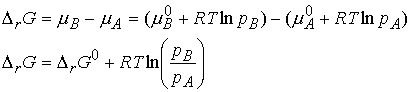
If we denote the ratio of partial pressures by Q, we obtain
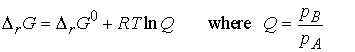
The ratio Q is defined as the reaction quotient. It ranges
from 0 (pure A) to infinity (pure B).
The standard reaction Gibbs energy, DrG° is defined as the
difference in the standard molar Gibbs energies of the products and
reactants.
![]()
We know that the difference in standard molar Gibbs energies of the products and reactants is equal to the difference in their standard Gibbs energies of formation, thus
![]()
At equilibrium, DrG = 0 and the
ratio of partial pressures is denoted as K
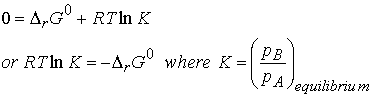
Molecular interpretation 9.1
In molecular terms, the minimum in the Gibbs energy, which
corresponds to DrG = 0, stems from
the energy of mixing of the two gases.
An important contribution to the position of chemical equilibrium is the
mixing of the products with reactants as the products are formed.
We see that when DrG° > 0, K < 1. Then at equilibrium, the partial pressure of A exceeds that of B,
which means that the reactant A is favored in the equilibrium. When DrG° < 0, K > 1 and B is favored at
equilibrium.
(d) A general reaction
For the general case the change in the amount of any species J is nJDx, where nJ is the
stoichiometric number of J in the chemical equation.
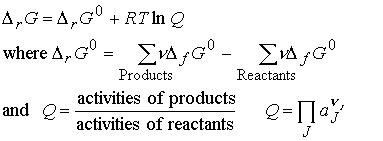
The P symbol to denote
product multiplication. Each species is
raised to a power given by its stoichiometric coefficient, n.
Recall that for pure solids and liquids, the activity is 1,
so there is no contribution to Q even though they may appear in the chemical
equation. For a gas, aJ = fJ/p0, where fJ is its
fugacity. For a perfect gas fJ = pJ, the partial
pressure of J.
Consider the reaction 2A + 3B ® C + 2D
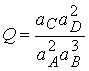
At equilibrium, the slope of G is zero: DrG = 0, and the
activities have their equilibrium values, so
![]()
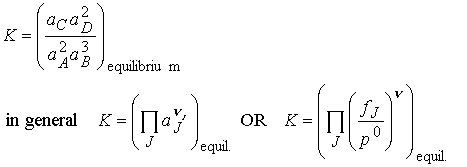
These expressions have the same form as Q but are evaluated
using equilibrium activities. An
equilibrium constant K expressed in terms of activities (or fugacities)
is called a thermodynamic equilibrium constant. Note that, because activities are dimensionless numbers, the
thermodynamic equilibrium constant is also dimensionless. We often can approximate activities with
concentrations and fugacities with partial pressures.
(e) The relation between equilibrium constants
To express the equilibrium constants in terms of mole fractions, xJ, or molalities bJ, of the species
we need to know the activity coefficients.
Recall
For example
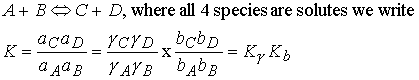
The activity coefficients must be evaluated at the equilibrium
composition of the mixture, which may involve a complicated calculation,
because the latter is known only if the equilibrium composition is known. In elementary applications we usually assume
Kg = 1.
Thus K is approximately = Kb. In chapter 10 we will show how
electrochemistry can be used to estimate activity coefficients.
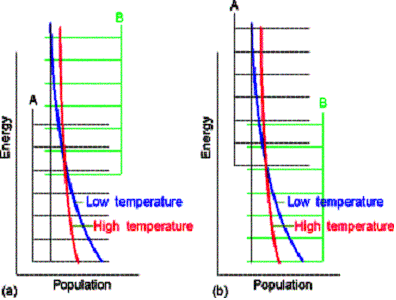
Molecular interpretation of equilibrum constants
Consider molecules of reactant A in the energy levels available to the molecule. In a large group (such as a mole of 1023 molecules) the statistical Boltzmann distribution of molecules over the available states shows a greater population (number) of molecules at lower energies, decreasing as the energy of the level increases.
At a given temperature, their will be a specific distribution of
populations, and hence a specific composition of reaction mixture.
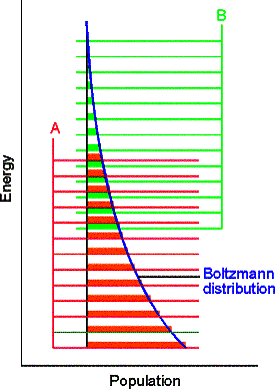

In the next figure, although B energy levels still lie higher than A energy levels, in this instance they are much more closely spaced. As a result, their total population may be considerable and B could even dominate in the reaction mixture at equilibrium. Closely spaced energy levels correlate with high entropy, so in this case we see that entropy effects can override a positive enthalpy. A positive enthalpy results in lowering the equilibrium constant
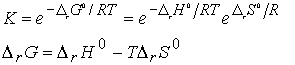
however a large, positive entropy may favor an equilibrium shifted to the reaction products, despite the endothermic character of the reaction.

Examples of closely spaced energy levels include non-rigid
molecules. Several conformations are
available with very little energy required to interconvert. This is the source
of the closely spaced energy levels.
For example, consider ethylene, H2C=CH2 has one
configuration while ethane, H3C-CH3 has three rotational
isomers with equivalent energy. Higher
entropy and closer spaced energy levels are expected for ethane.
The equilibrium constant for a catalyzed reaction changes
the reaction rate at which equilibrium is attained, but does not affect the
equilibrium position.
9.2 How equilibria respond to pressure
The equilibrium constant depends upon the value of DrG°, which is defined at a single
standard pressure. Therefore DrG°, and K
are independent of the pressure at which equilibrium is actually
established. Formally
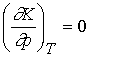
Even though K is independent of pressure, the equilibrium
composition can change. There
are two ways to increase the pressure of a reaction:
1. Add an inert gas
If the gas behaves ideally, the partial pressure of the products and
reactants do not change, hence the equilibrium composition stays the same.
2. Compression The pressure of a system can
be increased by confining the gases to a smaller volume. In this case, partial pressures will
change. Consider the case A Û 2B,

To remain constant, an increase in pA must offset an
increase in the square of pB. The number of A molecules will increase.
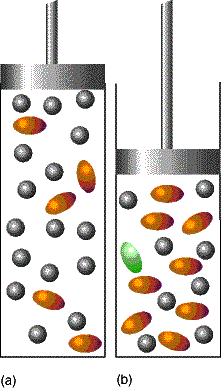

The increase in the number of A molecules and the corresponding
decrease in the number of B molecules brought about by compression is a special
case of LeChaelier's principle.
A system at equilibrium, when subjected to a disturbance,
responds in a way that tends to minimize the effect of the disturbance.
For instance compression of the previous case: the system will try
to minimize particles in the gas phase, A ¬ 2B.
The extent of dissociation a, of A into B is
inversely related to pressure. As p
is increased a decreases.
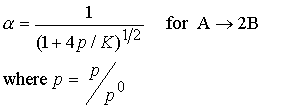
In
general, the composition will shift towards the side of the reaction with fewer
moles in the gas phase.
Illustration
To predict the effect of an increase in pressure on the composition of ammonia synthesis at equilibrium, we note that the number of gas molecules decreases (from 4 to 2). So LeChatelier's principle predicts an increase in pressure will favor product.
![]()
9.3 The response of equilibrium to temperature
LeChatelier's
principle predicts that a system at equilibrium will tend to shift in the
endothermic direction if the temperature is raised, for then energy is absorbed
as heat. Conversely, an equilibrium can
be expected to shift in the exothermic direction if the temperature is lowered,
for the reduction in temperature is opposed.
Exothermic reactions:
increased temperature favors the
reactants.
Endothermic reactions:
increased temperature favors the
products.
(a) The van't Hoff equation
An expression for the slope of a plot of equilibrium constant as a
function of temperature.
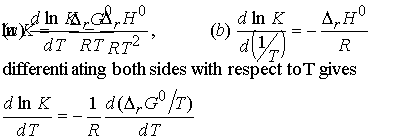
Justification 9.3
The differentials are complete because K and DrG0 depend only on
T, not p. From the Gibbs-Helmholtz equation
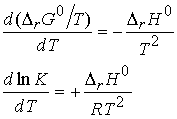
The b form is obtained by noting
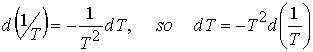
When reaction is exothermic under standard conditions
(DrH° < 0) ![]() .
.
A negative slope means that lnK, and therefore K itself, decreases as temperature rises.
Some insight into the thermodynamic behavior can be found in the
expression
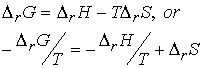
When the reaction is exothermic, -DH/T corresponds to
a positive change in entropy of surroundings, and favors formation of
products. When T is raised, -DH/T decreases, and
the increasing entropy of surroundings has a less potent role. As a result the equilibrium lies less to the
right.

When the reaction is endothermic, the principle factor is the
increasing entropy of the reaction system.
The importance of the unfavorable change of the entropy of the
surroundings is reduced if the temperature is raised (because DH/T is smaller),
and the reaction is able to shift towards products.
(b) The value of K at different temperatures.
We integrate to obtain
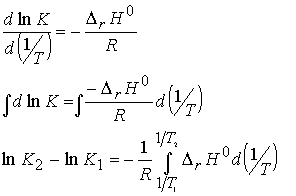
If we assume reaction enthalpy is constant over the temperature
range of interest, then we have
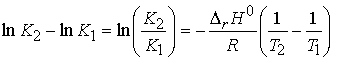
Illustration
To estimate the equilibrium constant for the synthesis of ammonia
at 500 K from its value at 298 K (6.0 x 105) we use the
standard reaction enthalpy (Table 2.6), ![]() (DfH°=0 for H2 and N2.) Then with DrH° = -92.2 kJ/mol,
we find
(DfH°=0 for H2 and N2.) Then with DrH° = -92.2 kJ/mol,
we find
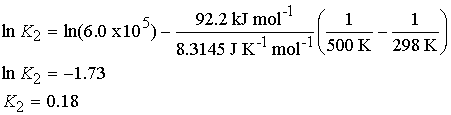
Acid-base equilibria in water
The only change is to use activity instead of concentration in the
equilibrium expression.
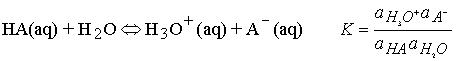
For dilute solution the activity of water is close to 1 (the value
of pure water), and the equilibrium can be expressed in terms of the acidity
constant, Ka :