Example 7.4 Using Henry’s Law

Estimate the molar solubility (the solubility in moles per liter) of oxygen in water at 25 ⁰C and a partial pressure of 160 torr (its partial pressure in the atmosphere at sea level). The Henry’s constant for O₂ in water at 298 K is 3.30 x 10⁷ torr.

Method The mole fraction is given by Henry’s law as

x_O = p_O/K, where p_O is the partial pressure of oxygen. Use mole fraction to solve for moles of O₂.

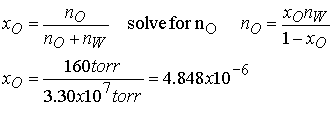
Since the mole fraction of O₂ is so low we can use the moles of pure water for the moles of water in the solution.

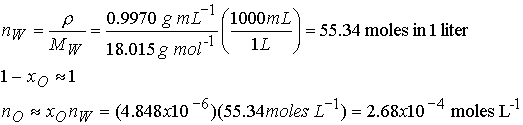
Divers have to be concerned about the solubility of O₂ and N₂ in blood since the concentration of dissolved gases in blood increases as pressure is increased. If a diver comes to the surface too quickly (where the solubility of N₂ is lower) the N₂ can form bubbles of gas in blood veins and capillaries and cause the pain of the bends. Deep sea divers breathe a mixture of 98% He, 2% O₂. He has a much lower solubility in blood than N₂. At a pressure of 10 atm this gives an O₂ partial pressure of about 0.2 atm (the pressure at atmosphere).

The properties of solutions

7.4 Liquid mixtures

Gibbs energy of mixing of two liquids calculated in the same way as for gases (7.2a)

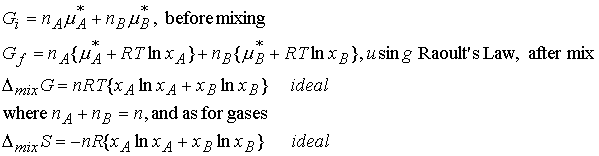
For perfect gases there are no interactions between the molecules. For ideal solutions there are interactions, however the A-A , A-B, and B-B interactions are all equal. The enthalpy of mixing is zero.

Real gases have different A-A, A-B, and B-B interactions. There may be an enthalpy change and possibly an entropy change when the liquids mix. Gibbs free energy can be positive or negative. In the case of DG > 0, the components spontaneously separate (immiscible). In some cases, the two liquids may be soluble over a limited range (partial miscibility).

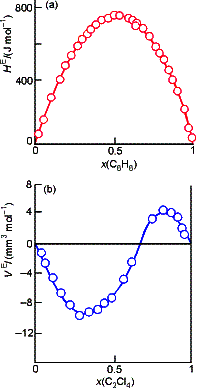
The thermodynamics of real solutions may be expressed in terms of excess functions, X^E, the difference between the observed thermodynamic function of mixing and the function of an ideal solution. For example, the excess entropy:

where D_mixS^ideal was given earlier. The excess enthalpy, H^E, and volume, V^E, are both equal to the observed enthalpy and volume of mixing, because the ideal values are zero in each case.

Deviations of the excess energies from zero indicate the extent to which solutions are non-ideal. We define a regular solution model. One in which the two types of molecules distribute randomly (S^E = 0), but have different energies of interaction (H^E not equal to 0).

7.5 Colligative properties

•Boiling point elevation

•freezing point depression

•osmotic pressure

Arise from the presence of solute particles independent of identity. Properties are proportional to the number of particles. The following expressions are derived with two assumptions:

1. solute is non-volatile ( has no vapor pressure in the solution)

2. the solid solvent and solute are immiscible (freezing pt. Depression)

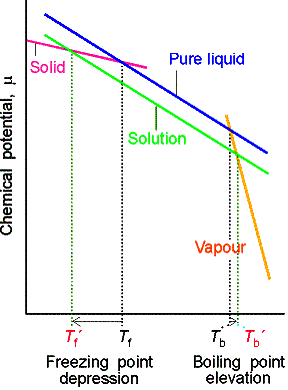
(a) The common features of colligative properties

All the colligative properties stem from the reduction of the chemical potential of the liquid solvent as a result of the presence of solute.

Molecular interpretation 7.3

The molecular origin of the lowering of chemical potential is not the energy of interaction of the solute and solvent molecules, because lowering occurs in ideal solutions (with zero enthalpy of mixing). It must be an entropy effect.

Boiling point elevation. The pure liquid solvent has an entropy which reflects the disorder of its molecules. Its vapor pressure reflects the tendency of solution towards greater entropy, which is achieved by vaporization into the more highly disordered gas phase. When a solute is present, there is an additional contribution to the entropy of the fluid (even in an ideal solution). The entropy of the solution is higher than that of the pure solvent and thus there is a weaker tendency to form the gas. The effect of solute appears as a lower vapor pressure and hence a higher boiling point.

Freezing point depression. Similarly, the enhanced molecular randomness of the solution opposes the tendency to freeze. Consequently, a lower temperature must be reached before equilibrium between solid and solution is achieved. Thus, the freezing point is lowered.

Strategy for quantitative discussion of boiling point elevation and freezing point depression is to find the temperature at which, one phase (pure solvent vapor or pure solid solvent) has the same chemical potential as the solvent in solution. This will be the new equilibrium temperature.

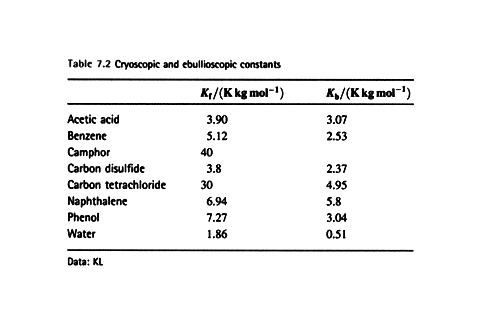
(b) The elevation of boiling point

We again denote the solvent by A and the solute by B for this heterogeneous equilibrium.

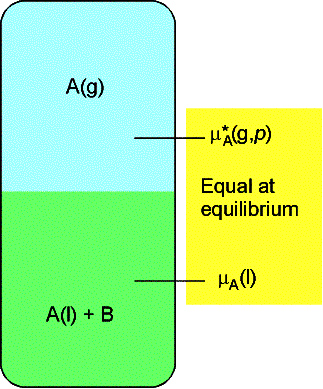
The equilibrium is established at a temperature for which

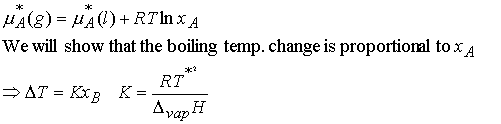
where T^* is the normal boiling point and DT is the boiling point elevation.

Justification 7.2

First substitute 1 – x_B = x_A and rearrange the equilibrium chemical potential expression.

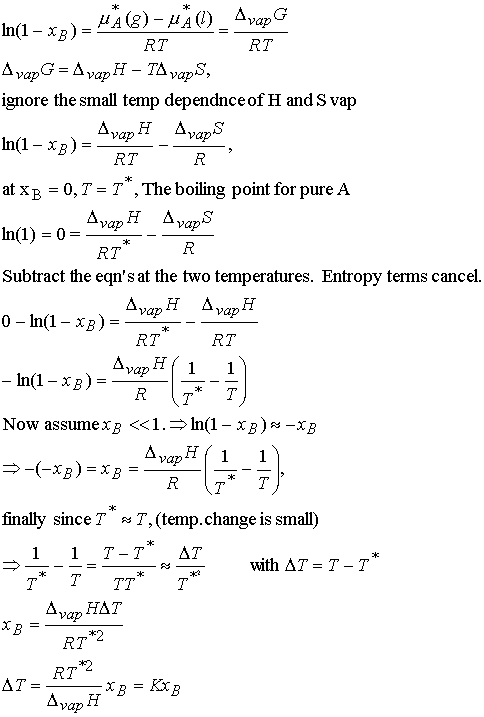
The value of DT does depend upon the properties of the solvent and not the solute. The biggest change occurs for solvents with high boiling points. For practical applications we note that the mole fraction of B is proportional to the molality, b, in dilute solution.

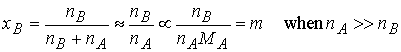
and write

where K_b is the empirical ebullioscopic constant of the solvent.