The thermodynamics of mixing

The dependence of the Gibbs energy of a mixture on its composition is given by . At constant T and p, systems tend towards a lower Gibbs energy. We will now quantitatively apply thermodynamics to the discussion of spontaneous changes of composition, as in the mixing of two substances. (two gases mix spontaneously, so G must decrease).

The Gibbs energy of mixing

Two perfect gases in two identical containers with amounts n_A and n_B, both at the same T and p.

The difference G_f -G_i , the Gibbs energy of mixing, D_mixG, is

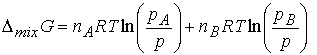
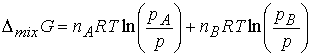
The chemical potential terms cancel because they don’t change in this process.

Now we use Dalton’s law to write n_J = x_Jn and p_J/p = x_J, so

Because mole fractions are never greater than 1, the logarithms are negative, and Gibbs energy of mixing < 0. Thus perfect gases mix spontaneously in all proportions.

Example

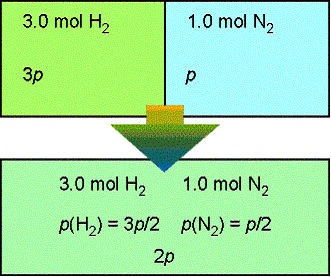
A container is divided into two equal compartments (figure below). One contains 3.0 mol H₂ at 25 ⁰ C.; the other contains 1.0 mol N₂ at 25 ⁰ C. Calculate the Gibbs energy of mixing when the partition is removed. Assume perfect gas behavior.

Method: We first calculate the initial Gibbs energy from

chemical potentials. We need the pressure of each gas. Let p = pressure of nitrogen, and the pressure of hydrogen can be found as a multiple of p. p can be computed from the gas laws. Next, calculate the Gibbs energy for the system when the partition is removed. The volume of each gas doubles so its partial pressure falls by a factor of two.

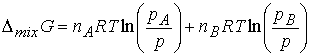
Answer: Use the expression for D_mixG

Given the initial pressure of nitrogen is p, the pressure of hydrogen is 3p; In the final state the partial pressure of nitrogen is p/2 and hydrogen is 3p/2. Therefore

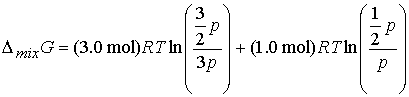
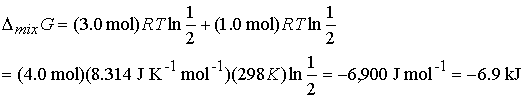
Other thermodynamic mixing functions

dG = -SdT + Vdp

Because it follows that D_mixS is

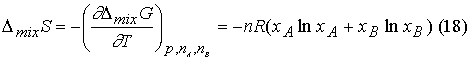
Because x <1, ln(x) is < 0, and so D_mixS > 0 for all compositions. Mixing of perfect gases is spontaneous.

The isothermal, isobaric enthalpy of mixing, D_mixH, of two perfect gases may be found from DG = DH - TDS.

D_mixH of real gases or liq.-liq., solid-liq. mixtures are non-zero. (eg. Ionic compounds in water)

7.3 The chemical potentials of liquids

We now investigate how the chemical potential of liquid mixtures vary with composition. We use the fact that at equilibrium the chemical potential of the liquid and vapor components are equal.

Ideal solutions

Convention: quantities relating to a pure substance will be denoted by a superscript *. No star – the mixture.

, or chemical potential of pure A (liquid)

chemical potential of A in the standard state

partial pressure of A. We’ll keep pressure in bar so that it can substitute for .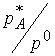

If another substance, a solute is present in the liquid, the chemical potential of A in the liquid is m_A and its vapor pressure p_A.

Next, we combine these two equations to estimate the standard chemical potential of the gas. Subtract the chemical potential of the vapor from the chemical potential of the liquid.

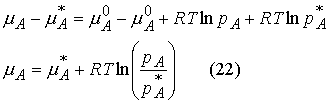
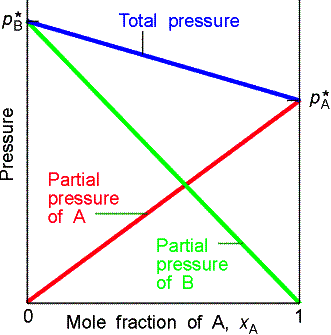
Raoult’s Law: For a liquid mixture the ratio of the partial vapor pressure of each component to its vapor pressure as a pure liquid, , is approximately equal to the mole fraction A in the liquid mixture.

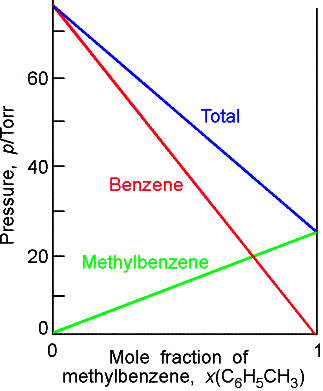
Mixtures that obey the law throughout are called ideal solutions.

For an ideal solution,

Solutions will most likely behave ideally when they are chemical similar.

Molecular interpretation

Consider the rates at which molecules leave and return to a liquid. Solute molecules at the air surface block some A molecules but in the gas the A molecules are not inhibited from condensing because of the low density of gases. The law reflects the fact that the presence of a second component reduces the rate at which A molecules leave the surface of the liquid but does not inhibit the rate at which they return.

The rate at which A molecules leave the surface is proportional to the concentration at the surface, which in turn is proportional to x_A:

rate of vaporization = kx_A

where k is a constant of proportionality. The rate at which molecules condense is proportional to their concentration in the gas phase, which is proportional to their partial pressure:

rate of condensation = k’p_A

At equilibrium, the rates of vaporization and condensation are equal, so k’p_A = kx_A.

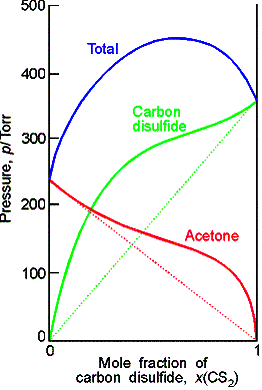
Ideal-dilute solutions

In ideal solutions the solute as well as the solvent obey Raoult’s law. For real solutions at low concentrations, although the vapor pressure of the solute is proportional to its mole fraction, the constant of proportionality is not the vapor pressure of the pure substance.

Henry’s law is: p_B = x_BK_B

In this expression K_B is an empirical constant (with dimensions of pressure) chosen so that the plot of the vapor pressure of B against its mole fraction is tangent to the experimental curve at x_B = 0.

Ideal-dilute solutions are mixtures for which the solute obeys Henry’s law and the solvent obeys Raoult’s law.

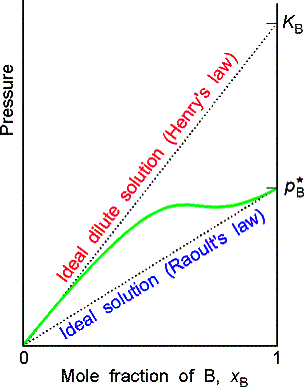
Molecular interpretation 7.2 The difference in behavior of the solute and the solvent at low concentrations arises from the fact that in a dilute solution the solvent molecules are in an environment very nearly like the pure liquid, but the solute molecules are in an environment very different from the pure solute.

Example of a chloroform-acetone mixture.

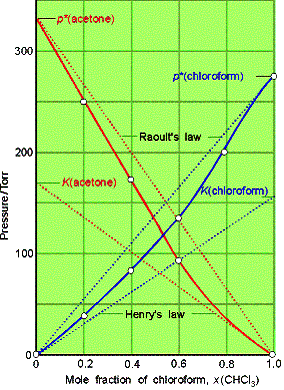
Example 7.4 Using Henry’s Law

Estimate the molar solubility (the solubility in moles per liter) of oxygen in water at 25 ⁰C and a partial pressure of 160 Torr (its partial pressure in the atmosphere at sea level).

Method The mole fraction is given by Henry’s law as

x_O = p_O/K, where p_O is the partial pressure of oxygen. Use mole fraction to solve for moles of O₂.

Since the mole fraction of O₂ is so low we can use the moles of pure water for the moles of water in the solution.

Divers have to be concerned about the solubility of O₂ and N₂ in blood since the concentration of dissolved gases in blood increases as pressure is increased. If a diver comes to the surface too quickly (where the solubility of N₂ is lower) the N₂ can form bubbles of gas in blood veins and capillaries and cause the pain of the bends. Deep sea divers breathe a mixture of 98% He, 2% O₂. He has a much lower solubility in blood than N₂. At a pressure of 10 atm this gives an O₂ partial pressure of about 0.2 atm (the pressure at atmosphere).