By the same argument that led to the total volume as a function of composition we can write

In an open system of constant composition, the Gibbs energy depends upon p, T, and composition(n_J). Thus the

equation dG = Vdp -SdT becomes

That is, non-expansion work can arise from the changing composition of a system. (electrical cell)

(c) The wider significance off chemical potential

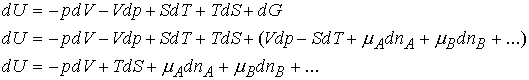
This expression is the generalization of

dU = TdS – pdV to include multiple components.

It follows that at constant volume and entropy,

Similarly,

Thus m_J shows how all the extensive thermodynamic properties U, H, A, and G, depend on the composition.

The Gibbs-Duhem equation

Because the total Gibbs energy of a mixture is given by

and the chemical potentials depend on the composition, when compositions are changed infinitesimally we write

At constant temperature and pressure,

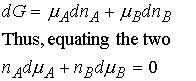
or more generally, the Gibbs-Duhem equation

The chemical potential of one component of a mixture cannot change independently of the other. In a binary mixture, if one partial molar quantity increases the other must decrease.

We can derive a similar equation for any other partial molar quantity. For example, the partial molar volume…

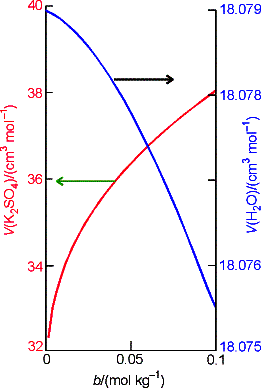
Example 7.1 Using the Gibbs-Duhem Equation

The experimental value of the partial molar volume of K₂SO₄(aq) at 298 K is given by the expression

where b is the numerical value of molality of K₂SO₄. Use the Gibbs-Duhem equation to derive an equation for the molar volume of water in the solution. The molar volume of pure water at 298 K is 18.079 cm³ mol^-1.

Let A denote K₂SO₄ and W denote water.

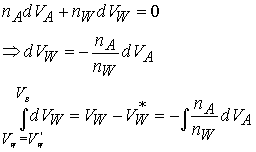
Next, change the variable V_A to the molality b. Take the derivative of V_A to get the differential of b. Then integrate the right hand side from b = 0 (pure water) to b.

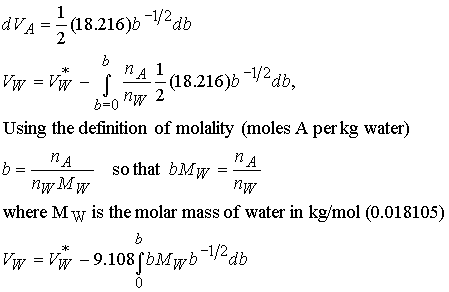
We have derived an expression for the molar volume of water (as a function of molality) from the molar volume of K₂SO₄ using their relationship in the Gibbs-Duhem equation.