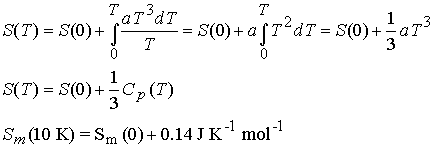The Clausius inequality.

So far we have proven S is a state function. We now need to verify that entropy is a signpost for spontaneous change.

Consider a system in thermal and mechanical contact with its surroundings at the same temperature, T (system & surroundings are not necessarily in mechanical equilibrium). Any change of state is accompanied by a change in entropy of the system, dS_sys, and of the surroundings, dS_sur. Because the process might be irreversible, the total entropy will increase when a process occurs in the system, we can write

The equality applies if the process is reversible.

When dq is the heat supplied to the system by the surroundings (dq_sur = -dq_sys).

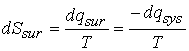
It follows that for any change,

The Clausius inequality

If the system is isolated from its surroundings, then dq_sys = 0, and dS_sys ³ 0 This implies that the entropy in an isolated system can not decrease when a spontaneous process takes place.

Example 1- A system undergoes irreversible adiabatic change:

dq = 0, and dS_sur = 0, & dS_tot ³ 0.

Example 2. - A perfect gas undergoes irreversible isothermal expansion freely into a vacuum. From ex. 4.1, dq = -dw, (because dU = 0). dw = 0 (vacuum), implies dq = 0, too. According to Clausius inequality, dS_sys ³ 0. For the surroundings, no heat is transferred, so dS_sur = 0, and in this case dS_tot ³ 0 also.

Example 3 Consider the irreversible process of spontaneous cooling.

Entropy of hot source changes by -½dq½/T_h (a decrease).
Entropy of the cold sink changes by +½dq½/T_c.

Overall entropy change is

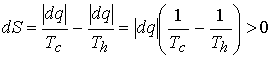
which is positive since, T_h ³ T_c. Hence cooling, the transfer of heat, is spontaneous.

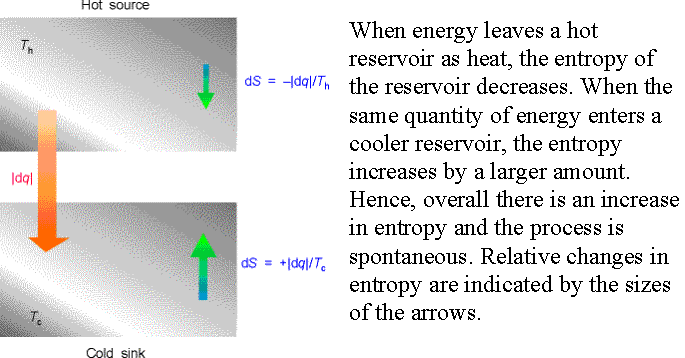
Entropy change is proportional to temperature. For the same heat transfer, dq, entropy change is larger for the lower temperature. (A more pronounced effect at lower temperature the system is more organized and has fewer modes of heat dissipation at lower temperature.

Entropy changes accompanying specific processes.

a) Entropy of phase transition at transition temperature

For liquid vaporization, the substance goes from a more compact dense phase with more order to a widely dispersed gas. We expect an increase in entropy to accompany this transition.

Consider an equilibrium mixture of water and ice at 273 K, (the normal transition temperature T_trs,) and 1atm. At the transition temperature, any transfer of heat between the system and surroundings is reversible because the two phases in the system are in equilibrium. At constant pressure, q = D_trsH_m

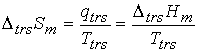
If the phase transition is exothermic (D_trsH < 0, as in freezing or condensing), then entropy is negative. The system has become more ordered. If the transition is endothermic, enthalpy positive, the entropy change is positive. This is consistent with the system becoming more disordered.

The entropy of system can be negative as long as DS_sur is equal or larger and positive so that DS_tot obeys the Clausisu inequality.

Some experimental entropies of transition.

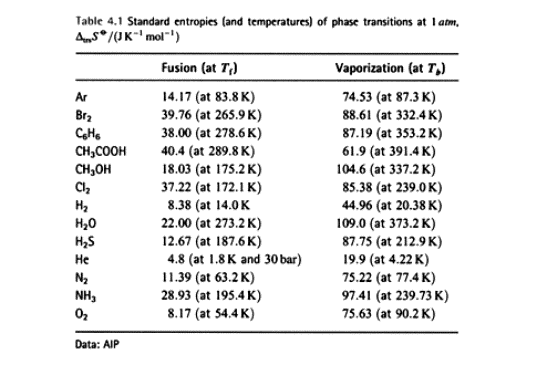
Interesting feature: a large number of fluids give ~ the same standard entropy of vaporization ( about 85 J K^-1) - Trouton’s Rule (a rule of thumb)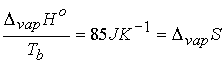

Molecular interpretation of Trouton’s rule.

A comparable amount of disorder is generated when any liquid evaporates and becomes a gas. (most liquids similar)

Some do not follow the rule (such as water and alcohols) which are more ordered in the liquid due to hydrogen bonding.

Example 4.2 Using Trouton’s rule

Predict the standard molar enthalpy of vaporization of bromine using Trouton’s rule given that it boils at 59.2 ⁰C.

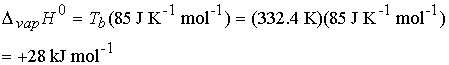
The experimental value is +29.45 kJ mol^-1.

b) The expansion of a perfect gas. Isothermal expansion

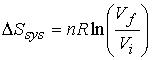
Since S is a state function, the expression above applies whether the transition is reversible or irreversible.

For reversible change DS_tot = 0, therefore DS_tot = -DS_sys

For irreversible change such as free expansion w = 0 and if T remains constant, then q = 0. Therefore, DS_sur = 0
and DS_tot = DS_sys.

c). The variation of entropy with temperature

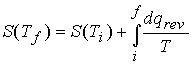
At constant pressure, with no expansion work,

Consequently,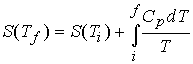

At constant volume

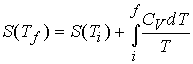
IfIf If C_p can be considered constant

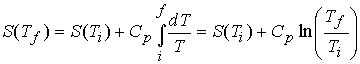
Example Calculate the entropy change when argon at 25 ⁰ C and 1.00 atm in a container of volume 500 cm³ is compressed to 50.0 cm³ and is simultaneously cooled to -25⁰ C.

Method: Since S is a state function we can choose any convenient reversible path. We will break the process into two reversible steps. First step is reversible isothermal compression to the final volume followed by the second step, reversible cooling at constant volume to the final temperature.

We need to compute n from the ideal gas law. ^{Use 1 L = 1 dm3}

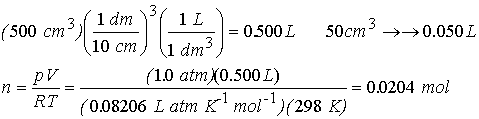
Step 1 reversible, isothermal compression

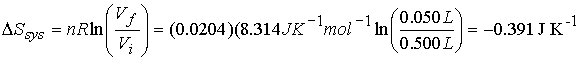
Step 2 reversible cooling at constant volume

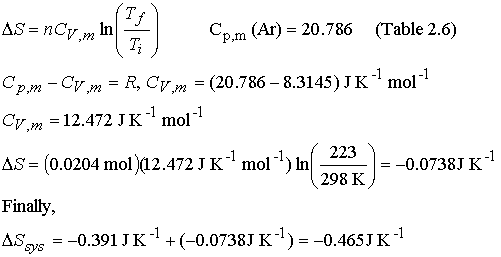
The entropy of the system decreases as it is cooled and compressed, both increase the order of the molecules, fewer molecular states are available.

Measurement of entropy

The entropy of a system at temperature T is related to its entropy at T = 0 by measuring its heat capacity, C_p, at different temperature ranges and evaluating the following integral.

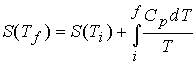
Entropy of transitions must be added (D_trsH/T_trs), for example a substance that melts (T_f ) and boils (T_b).

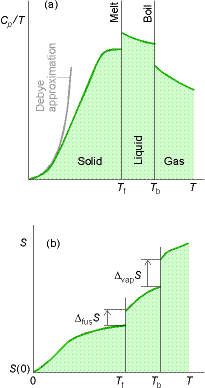
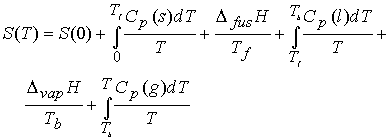
Heat capacities are difficult to measure near zero T. The Debye Extrapolation indicates that heat capacities at low T follow the following relationship

C_p is determined at as low a T as possible and the data is fit to the function aT³ to determine a .

Metals at very low temperature also have a contribution to the heat capacity from the electrons. At low enough temperature the free flow of electrons (conduction) becomes restricted. The molar heat capacity is linearly proportional to temperature.

Example 4.4 Calculating the entropy at low temperatures.

The molar constant-pressure heat capacity of a certain solid at 10 K is 0.43 J K^-1 mol^-1. What is its molar entropy at that temperature?