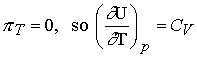Chapter 3   First Law: The Machinery

 

The Mathematics of Thermodynamics:

 

The power of thermodynamics is in being able to relate measurable properties to those that are not so easily measured.  Many of the relationships involve the slopes of functions, the rate of change of one variable with respect to another, the derivative.  To understand how these relationships are derived we need to understand some mathematical properties of differentials and partial derivatives.  See Further Information 1, pg. 905-906.

 

Exact differentials

Recall that change in internal energy, dU, is called an exact differential because it depends only on initial and final state of the system but not the path.  We will define exact differential mathematically.

 

If we have a function arbitrarily designated by J which depends upon the variables T and p so that we may write J = J(T, p), then the infinitesimal change in J, dJ, is given by


 


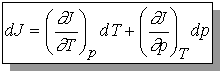
The variables T and p must be independent and J(T,p) must be continuous, single-valued, differentiable.

(no step functions, one value of J for every T and p, no functions with cusps)

 

 

 

 

The partial derivatives will, in general, also be functions of T and p, derivable from J(T,p) by standard differentiation techniques. We could therefore define the functions M and N by


 

 

 


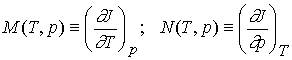
The expression for dJ becomes    dJ = MdT + Ndp

 

We know that the order of differentiation doesn’t matter for second derivatives.    

   

 

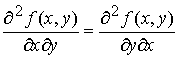
If the original function J(T,p) is continuous, single-valued and differentiable, then

 

 


 


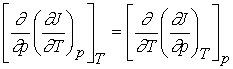
Inserting M and N for their differentials


 

 


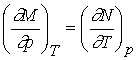
This condition is sufficient as well as necessary for an exact differential.  That is, given an expression in differential form P(Q,S) and R(Q,S),

if 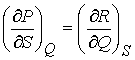         then there exists a function f(Q, S)  such

that df = PdQ + RdS. 

 

If these conditions are met, then df is called an exact differential.

 

If the function f(Q, S) is single-valued; that is, if for each set of values of Q and S one and only one value of f exists, then changes in f as Q and S change depend only upon the initial and final values of Q and S.  That is, we may write

 


 

 


in which the last expression means “Df is a function only of Q1, Q2, S1 and S2”. 

 

Line integrals

Another way we could evaluate changes in the function f is to integrate the differential.  We may write


 

 


Since the differential df is exact, this integral will depend only upon S1, Q1, S2, and Q2.  There are an infinite number of ways we can go from S1, Q1 to S2, Q2 since these are completely independent variables.  For example we may hold S constant at S1 while changing Q from Q1 to Q2, and the hold Q constant at Q2 while varying S from S1 to S2.

 


 

 


This is called a path.  The integral of an infinitesmal quantity along such a path is called a line integral.  The form of the integrals will be different for different paths but the line integral of an exact differential depends only on the initial and final values of the independent variables and not upon the path of integration. 

 

 

Let’s test a differential for exactness.

Example 1


 

 


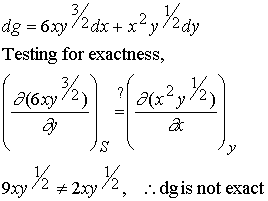
Example 2:  Show that the differential dVm of the molar volume of an ideal gas is an exact differential.  

 

First write the differential expression.

 

 

     

 


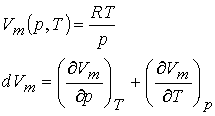
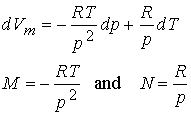
Then take the first partial derivatives

 

 


Finally take the second partial derivatives


 


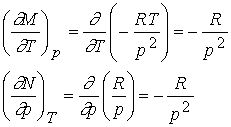
They are equal so Vm is an exact differential.  Therefore Vm is a state function and depends only on initial and final state.

 

 

We will use some other relationships (identities) for partial derivatives (pg. 906).

 
State functions and exact differentials

 

 

                                                        


 

 

 

 

 

 


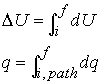    dU depends only on the initial and final states. dU is exact.  q is the sum of the individual contributions of  heat transferred at each point along a path.  dq is inexact.

 

 

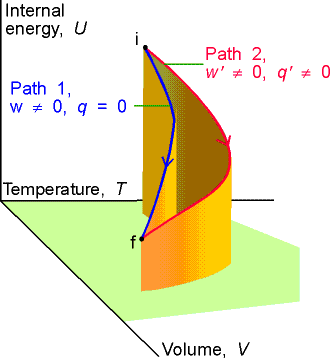
Calculating work, heat, and internal energy

Consider a perfect gas inside a cylinder fitted with a piston.  Let the initial state be T, Vi and the final state be T, Vf. The change of state can be brought about in many ways, two of which are: Path 1, in which there is irreversible isothermal expansion against a constant pressure; Path 2, in which there is reversible, isothermal expansion.  Compute w, q, and DU for each path.

 

DU = q + w

DU = 0   for any isothermal change of a perfect gas.

q = -w

 

Path 1.  irreversible

w = -pexdV   so  q = + pexdV

                 


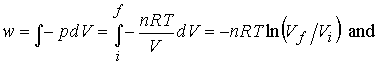
Path 2.  reversible


 


We see that DU is the same for each path but q and w are different by paths 1 and 2.

 

 

 

 

 

Changes in internal energy


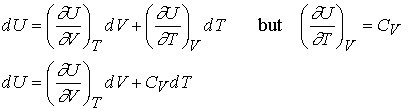
For a closed system, constant n, U is a function of volume and temperature.  Now suppose that V and T both change infinitesimally

 

 


 


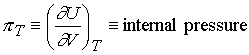
Internal pressure is a measure of the strength of the cohesive forces of the sample (intermolecular forces)

 

 


 

 

 


 

 

 

 

 

 


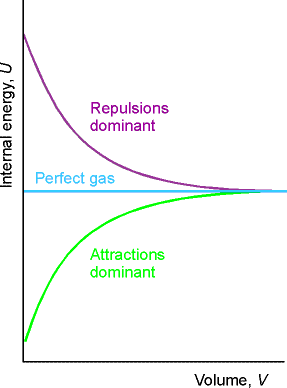
Illustration

For ammonia, pT = 840 Pa at 300 K and 1.0 bar, and CV,m = 27.32 J K-1 mol-1.  The change in molar internal energy of ammonia when it is heated through 2.0 K and compressed through 100 cm3 is ~

 

 


 


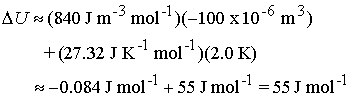
Note that the heating term dominates the internal energy

 

 

Changes in internal energy at constant pressure

How does internal energy vary with temperature when the pressure of the system is constant.

 


 

 


Divide both sides by dT and impose constant pressure gives

 


 

 

 

 


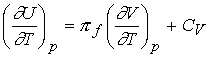
Defining the expansion coefficient, a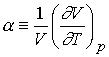   

gives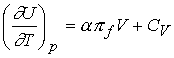   

 

A large value for a means the volume responds strongly to changes in temperature.

 

 

Example - using the expansion coefficient of a gas

 

Derive an expression for the expansion coefficient of a perfect gas. 

 

 


 

 


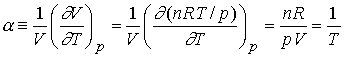
The internal pressure for a perfect gas is zero, non-interacting.