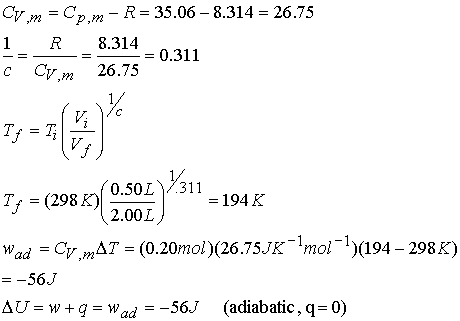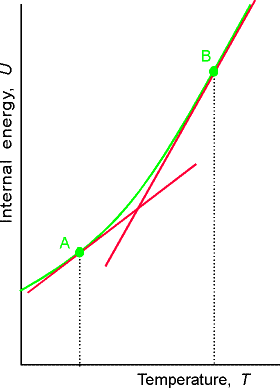
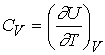
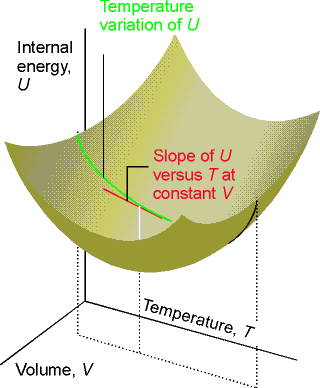
Over small temperature ranges the slope changes very little – C_v may be considered a constant.

Heat capacity is an extensive property. Molar heat capacity, C_v,m is an intensive property. (units J K^-1 mol^-1)

Specific heat capacity is the heat capacity divided by mass. (units J K^-1 g^-1 = J °C^-1 g^-1)

In general, heat capacities depend on temperature and decrease at low temperatures.

The heat capacity for a monatomic perfect gas is:

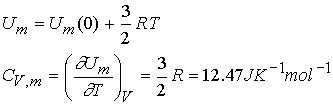
It follows that: dU = C_VdT and DU =C_VDT = q_V

Enthalpy: The change in internal energy is not equal to the heat supplied when the system is free to change its volume. Some energy is returned to the surroundings as expansion work so

dU < dq.

H = U + PV

P and V are the pressure and volume of the system. Enthalpy is a convenient state function for systems under constant pressure.

The change in Enthalpy is equal to the heat supplied to the system (so long as the system does no additional work).

dH = dq (at constant pressure, no additional work)

DH = q_p macroscopic measurement

Justification

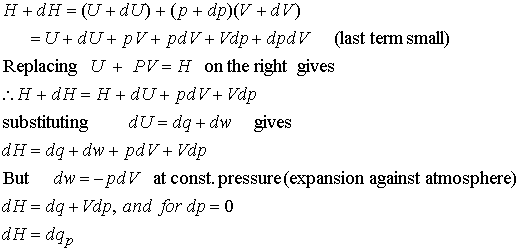
Measurement of enthalpy change: Calorimetry - measuring temperature change accompanying a chemical reaction at constant pressure. Another route is to use bomb calorimetry for solids and liquids where pV is small and dU » dH.

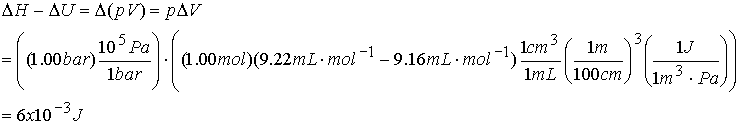
Example of relating DH and DU:

Calculate DH - DU for heating 1.00 moles of zinc(s) from 25 ^°C to 98 ^°C at 1.00 bar. The Zn undergoes a volume change from 9.16 mL mol^-1 to 9.22 mL mol^-1.

DU is typically a value in kJ so pressure/volume work (pV) is negligible.

For a perfect gas undergoing the same T increase,

the result is = 607 J

For a perfect gas:

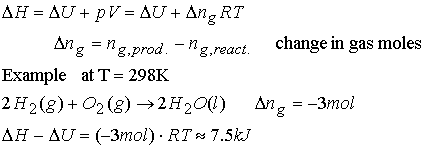
Example: Calculating a change in enthalpy

Water is heated to boiling under pressure of 1.0 atm. When an electric current of 0.50 A from a 12 Volt supply is passed for 300 seconds through a resistance in thermal contact with the water, it is found that 0.798 g of water is evaporated. Calculate molar internal and enthalpy changes at the boiling point (373.15 K).

Constant pressure: Enthalpy = heat supplied

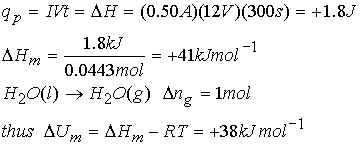
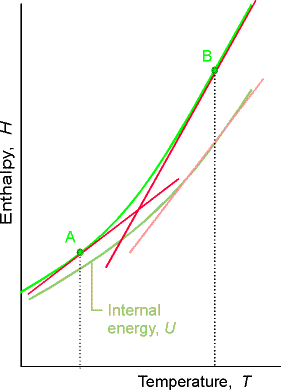
Variation of enthalpy with temperature:

Enthalpy increases with temperature at constant pressure. The heat capacity at constant pressure is defined as:

C_p is a function of temperature and can be approximated by the

following expression

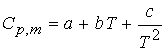
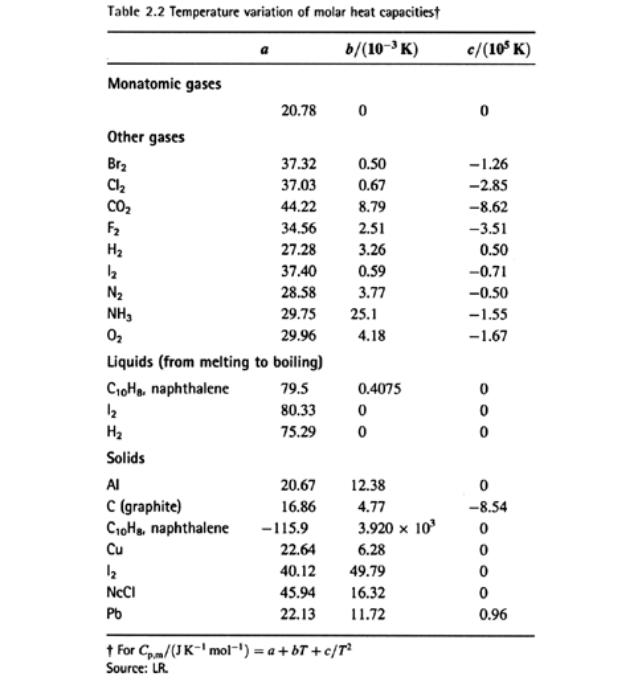
Example: What is the change in molar enthalpy of carbon dioxide when heated from 25 ^°C to 100 ^°C ?

For CO₂ a = 44.22, b = 8.79 x 10^-3, c = -8.62 x 10⁵

C_p,m = a + bT + cT^-2

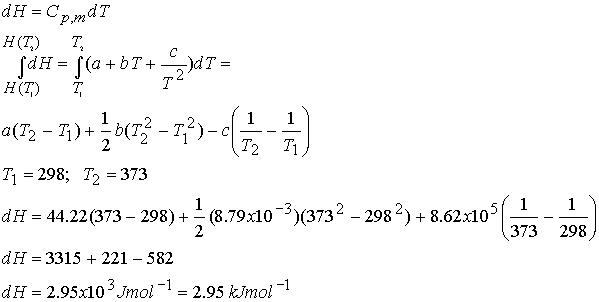
Relationship between heat capacities:

The constant pressure heat capacity (C_p) of a sample is greater than the constant volume heat capacity because in the former case the energy supplied as heat is used to do work of expansion, both against external pressure and (if there are intermolecular forces) against the cohesive forces within the sample. For a perfect gas

will be derived later.

C_p,m= C_v,m + R

For a monatomic gas C_v,m = 3/2R

So C_p,m = 3/2R + R = 5/2R

Adiabatic changes:

When a perfect gas expands adiabatically (q = 0)

we now expect T to decrease because:

•work is done

•the internal energy falls

•therefore the temperature of the working gas falls

The work of adiabatic change:

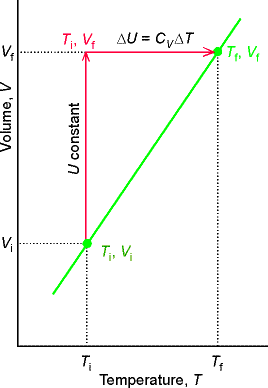
To achieve a change of state from one temperature and volume to another temperature and volume, we may consider the overall change as composed of two steps. In the first step, the system expands at constant temperature; there is no change in internal energy if the system consists of a perfect gas. In the second step, the temperature of the system is increased at constant volume. The overall change in internal energy is the sum of the changes for the two steps.

Because the internal energy of a perfect gas arises solely from the kinetic energy of the molecules, overall change in internal energy arises from the second step.

For an adiabatic process, q=0 by definition.

DU = q + w = w_ad

DU = C_VDT (provided C_V is independent of temp.)

w_ad = C_VDT

For the important case of an adiabatic reversible expansion relate the change in volume to the change in temperature.

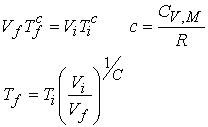
Use this expression to determine temperature change from the volume change.

Prove the equation.

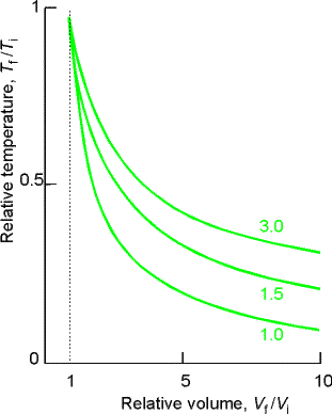
Example: Consider the adiabatic reversible expansion of 0.20 mol NH₃, initially at 25 ⁰C, from 0.5 L to 2.00 L. C_p,m for NH₃ = 35.06 JK^-1mol^-1, so c = 1.501. Determine the final T, DU, and w.