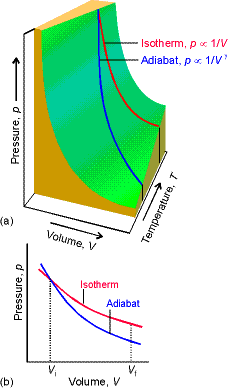
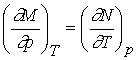Heat capacity ratios and adiabats:

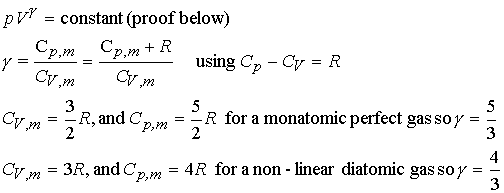
Consider Dp for an adiabatic, reversible expansion of a perfect gas.

Proof

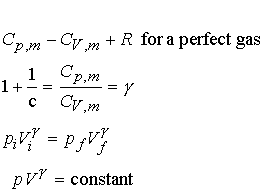
Thermochemistry:

The study of heat produced or required for chemical reactions.

Calorimetry is used to measure heat:

-at constant volume q_V = DU , internal energy

-at constant pressure q_p = DH, enthalpy

*If we know DU or DH for a reaction, we can predict the heat that will be produced.

Define: Standard enthalpy change = DH⁰, where initial and final substances are in their standard state.

Standard state of a pure substance is 1 bar.

Example: standard enthalpy of vaporization

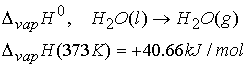
All kinds of enthalpies- Enthalpies of physical change

Standard enthalpy of transition = is the standard enthalpy for a physical change.

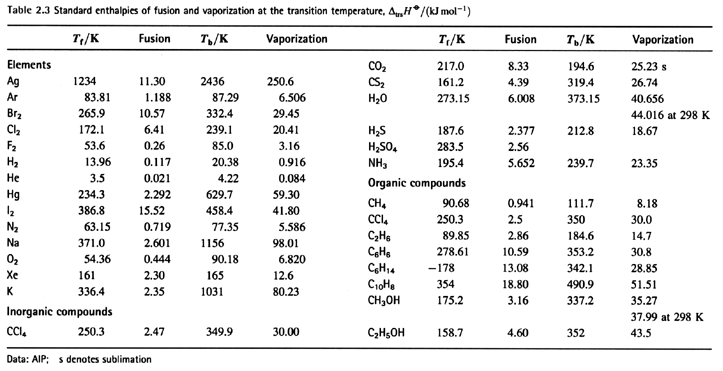
Enthalpy is a state function which is independent of path. This is very significant in thermochemistry.

solid ® vapor (sublimation)
solid ® liquid ® vapor Same enthalpy for both!

Also, as a state function,

Enthalpies of chemical change:

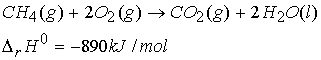
Standard reaction enthalpy = D_rH⁰

The combination of a chemical reaction and a standard reaction

enthalpy is called a thermochemical equation.

Consider 2A + B ® 3C + D

Example:

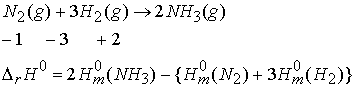
Hess’s Law: The standard enthalpy of an overall reaction is the sum of the standard enthalpies of the individual reactions into which a reaction may be divided.

The standard enthalpy of formation, D_fH⁰, of a substance is the reaction enthalpy for the formation of the compound from its elements in their reference states.

The reference state of an element is its most stable state at the specified temperature and 1 bar. Example - benzene @ 298 K

The standard enthalpies of formation for the elements in their reference state are 0 at all temperatures. ie

Reaction enthalpy in terms of enthalpies of formation. Conceptually regard a reaction as proceeding by decomposing the reactants into their elements and then forming those elements into products. The value of D_rH⁰ is the sum of the forming and unforming enthalpies.

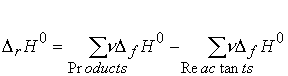
Illustration:

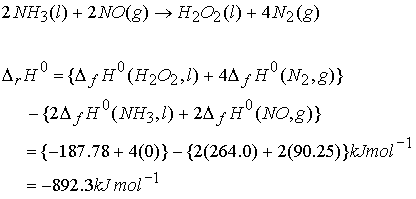
Formally,

Example of Hess’s Law:

D_rH^o = -124 +(2220) + -(-286) = -2058 kJ mol^-1

Thermochemical Group Contributions:

An approach to compute standard reaction enthalpies from knowledge of the composition of the chemical species.

A molecule is regarded as being built up of thermo-
chemical groups. The enthalpy of formation of the
the compound is then expressed (approximately) as the

sum of the contributions associated with all the

thermochemical groups of the molecule.

Example: Thermochemical group approach.

Estimate of standard enthalpy of formation at 298 K of 2,2-dimethylpropane in a) the gas phase, b) the liquid phase.

First, identify the thermochemical groups present in the molecule.

There are four CH₃(C) groups and one C(C)₄ groups.

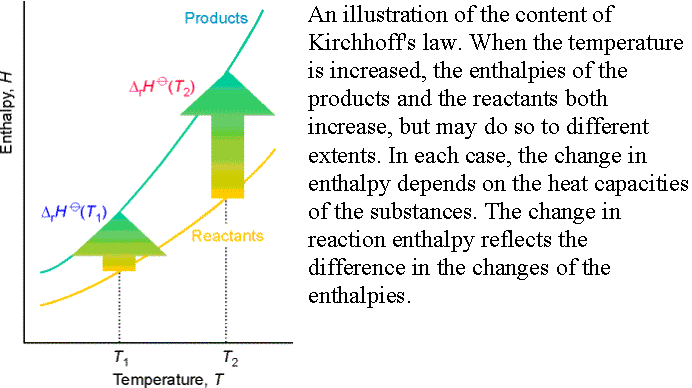
Temperature dependence of reaction enthalpies:

In the absence of standard enthalpy data for a substance at a given T, it can be estimated from heat capacities and the reaction enthalpy at some other temperature.

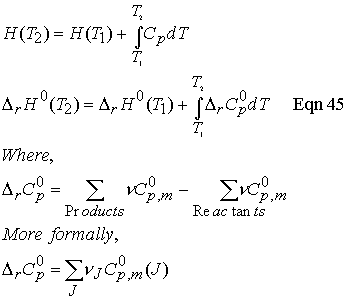
Equation 45 is known as Kirchhoff’s law and is normally a good approximation to assume D_r Cp is independent of temperature.

Example: The standard enthalpy of formation of gaseous H₂O at 298 K is -241.82 kJ mol^-1. Estimate the value at 100 ⁰C given the following values of molar heat capacities at constant pressure: H₂O(g) : 33.58 kJ mol^-1; H₂ (g) : 28.84 kJ mol^-1; O₂ (g) : 29.37 kJ mol^-1. Assume heat capacities are independent of T.

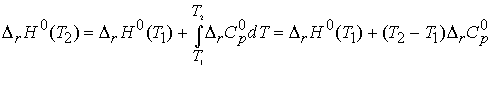
Chapter 3 First Law: The Machinery

The Mathematics of Thermodynamics:

The power of thermodynamics is in being able to relate measurable properties to those that are not so easily measured. Many of the relationships involve the slopes of functions, the rate of change of one variable with respect to another, the derivative. To understand how these relationships are derived we need to understand some mathematical properties of differentials and partial derivatives. See Further Information 1, pg. 905-906.

Exact differentials

Recall that change in internal energy, dU, is called an exact differential because it depends only on initial and final state of the system but not the path. We will define exact differential mathematically.

If we have a function arbitrarily designated by J which depends upon the variables T and p so that we may write J = J(T, p), then the infinitesimal change in J, dJ, is given by

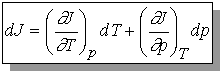
The variables T and p must be independent and J(T,p) must be continuous, single-valued, differentiable.

(no step functions, one value of J for every T and p, no functions with cusps)

The partial derivatives will, in general, also be functions of T and p, derivable from J(T,p) by standard differentiation techniques. We could therefore define the functions M and N by

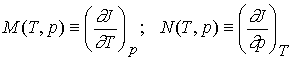
The expression for dJ becomes dJ = MdT + Ndp

We know that the order of differentiation doesn’t matter for second derivatives.

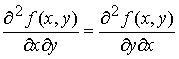
If the original function J(T,p) is continuous, single-valued and differentiable, then

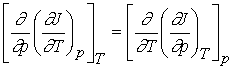
Inserting M and N for their differentials