The Mole fraction, x_j , is the amount of J expressed as a fraction of the total amount of molecules, n, in the sample.

x_J = n_J / n where n = n_A + n_B + .....

It follows that x_A + x_B + .... = 1

We define Partial Pressure p_J , of a gas J in a mixture ( perfect or real) as p_J = x_Jp , where p is total pressure.

Also p_A + p_B + ..... = (x_A + x_B + .... ) p = p

Example 1:

The pressure of a gaseous mixture of NH₃ and N₂ decreased from 1.5 kPa to 1 kPa after all the NH₃ was absorbed from the mixture. Assume ideal gas behavior and find initial composition of the mixture.

Partial pressure of N₂ is 1 kPa , P_T = P_NH + P_N

P(NH₃) = P_T - P(N₂) = 1.5 kPa - 1 kPa = 0.5 kPa

from Dalton’s Law : x(N₂) = P(N₂)/P_T = 1 kPa/1.5kPa = 0.67

x(NH₃) = 1- x(N₂) = 0.33

Example 2:

The mass composition of dry air at sea level (in g%) is (N₂): 75.52, (O₂): 23.15, (Ar): 1.28, (CO₂): 0.046. What are the partial pressures at 0.90 atm total p?

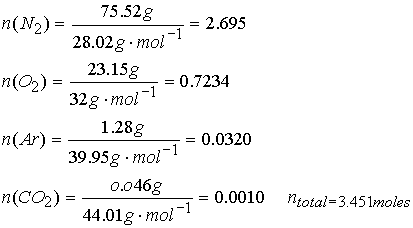
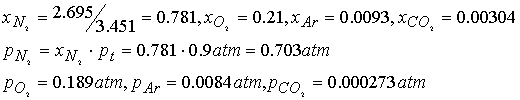
The ideal gas law is derived using the ideas from the kinetic model of gases.

Assumptions:

1. gas molecules are in ceaseless random motion

2. molecular size is negligible (molecular diameter << average collision distance)

3. molecules do not interact; elastic collisions (like billiard balls)

Given this picture of gas molecules one can derive expressions for the average speed of molecules as a function of pressure, temperature and volume.

The (ideal) perfect gas law then best predicts the behavior of a gas at low pressure and moderate temperature. The low pressure keeps molecules away from each other and the moderate temperature keeps their kinetic energy too high to stick to each other when they do collide.

Real Gases

Real gases deviate from ideal gas law equation because molecules interact with each other.

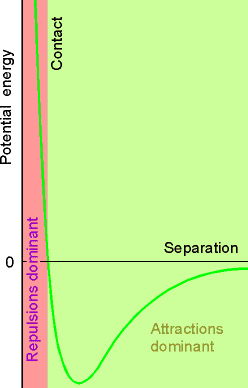
Fig. 1.21

•repulsive forces significant at short range (high pressure, close)

• attractive intermolecular forces ( relatively long range ),

important when molecules are fairly close together. Also when temp is very low, slow molecule speeds allow attractive forces to be more dominant.

Characterizing Real Gases

The distance dependence of the intermolecular forces can be characterized by plotting the compression factor, Z, against pressure, where Z is defined as

For a perfect gas Z = 1 under all conditions, deviation of Z from 1 is a measure of departure from perfect behavior.

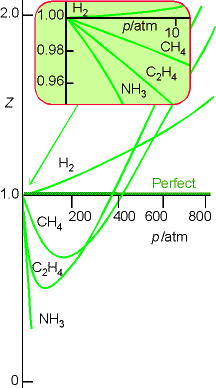
Fig. 1.22

Many equations have been developed to do a better job of predicting the P,V,T behavior of real samples of gases. We will discuss a few. They all work well in certain conditions.

Virial Coefficients

At large molar volumes & High T’s real isotherms do not differ greatly from ideal gas isotherms. Suggested form for real gas:

An example of a simple law treated with the first term in a series in powers of a variable (p).

A more convenient expansion/form:

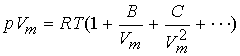
The coefficients B & C, virial coefficients, are experimentally derived and depend on T. C less important than B at typical molar volumes.

Compare the virial equation with the definition of the compression factor, Z.

As P goes to 0, for a real gas, the value for dZ/dp = 0 for a perfect gas, but for some real gases

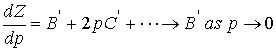
the slope of Z may not approach 0 because , B^’ ¹ 0

Similarly,

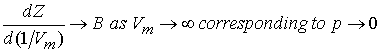
Since virial coefficients depend on T, there may be a T for which Z = 1 with zero slope @ low p or high V_m. At this temperature, T_B (Boyle Temperature), the properties of the real gas coincide with those of the perfect gas as p tends to 0. Z has zero slope as p ® 0 if B = 0 at the Boyle temperature.

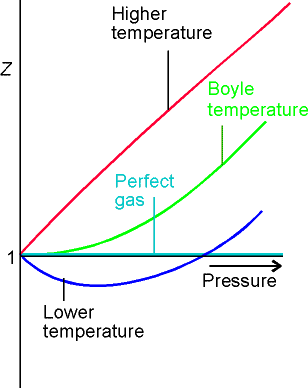Fig. 1.24

Example: What is the V_m of N₂ at 600 K and 600 bar?

a.) according to ideal gas, and b.) virial equation

B(N₂) @ 600K = 0.0217 L mol^-1

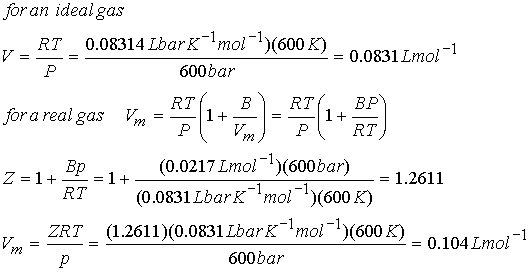
Condensation:

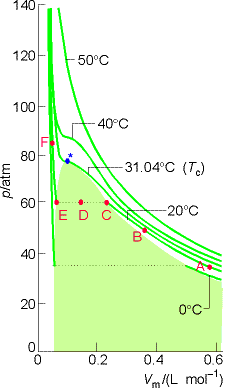
The pressure at the two phase region (EDC) is called the Vapor pressure of the liquid at the temperature of the experiment. The * @ T_c (31.04 ⁰C for CO₂) is a special temperature in the theory of matter. At less than T_c , the isotherm shows the two phase liq/gas equilibrium region.

At T = T_C, phase separation does not occur and the volumes of each end of the isotherm merge to a single point, the critical point of the gas. The p, T, and V at the critical point are called the critical temperature, T_c , the critical pressure, p_c, and the critical molar volume, V_c.

At and > T_c, the fluid occupies the entire volume of the container. The liquid phase will not form above T_c, and the gas phase is at this region is called a supercritical fluid. It is denser than a normal gas but not considered a liquid. Supercritical CO₂ is used as a solvent for extraction and chromatography.

The van der Waals equation

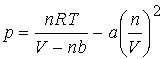
J. H. van der Waals 1873

The constants a & b are called the van der Waals coefficients. a & b are not a function of T.

Excellent example of physical model/equation derivation.

1. When repulsion's are significant, small impenetrable spheres that take up space suggest actual volume is V - nb. (Volume of the molecules is no longer negligible.)

2. Pressure depends on both frequency and speed of collisions. These are reduced by attractive forces that act proportional to molar conc. (mol/L), n/V.

Since frequency and force are reduced by the attractive forces, the pressure is reduced in proportion to the square of the concentration, - a (n/V)².

What is the molar volume of water @ 1.01325 bar and 100.0 °C.? Use van der Waals equation.

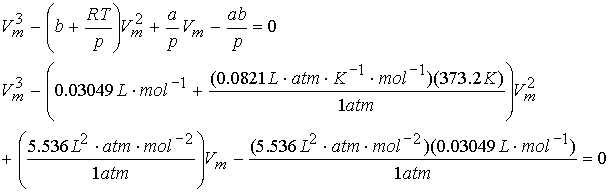
a = 5536 L² atm mol^-2, and b = 0.03049 L mol^-1

note cubic equation with 3 roots!

Use excel solver. V_m = 30.49 L/mol

The reliability of the van der Waal equation

Optimistic for one equation to describe many real gases. (however, it is an analytical expression)

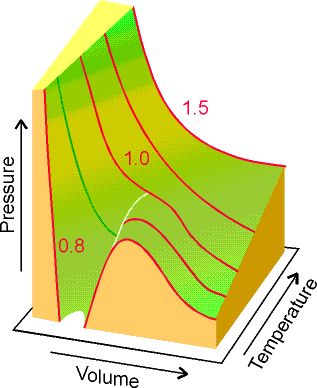
Figure 1.23 Figure 1.25

Real data on CO₂ van der Waal equation

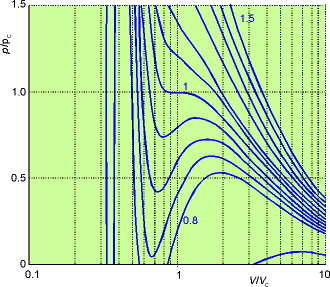
Figure 1.26

Apart from the oscillations below the critical point, they do

resemble experimental isotherms quite well. The red

line is a tie line where both liquid and gas exist.