Features of van der Waal isotherms:
1. Perfect isotherms at high T and large Vm.
2. Liquids and gases coexist when cohesive and
dispersing effects are in balance.
3. Critical constants are related to the van der Waals
coefficients. For T<Tc, calculated isotherms oscillate.
The oscillations converge as T approaches Tc. At
the critical point the curve has a flat inflection.
We can derive expressions for the critical constants from the van
der Waal equation.
First and second
derivative must be zero at inflection.
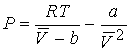
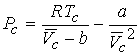
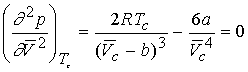
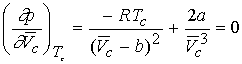
Combining the three equations gives a & b
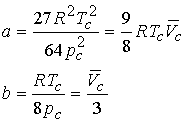
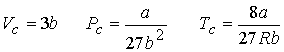
The values for a and b can be tested by predicting
the critical compression factor Zc for all gases.
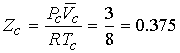
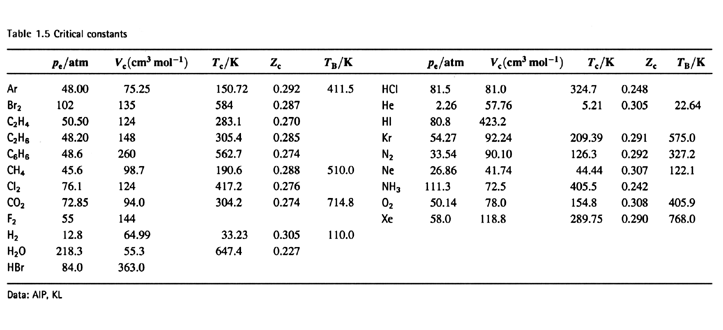
From the table Zc < 3/8 (~0.30) and fairly
constant. Small difference, good
agreement for many gases.
Principle of corresponding states:
Important general technique in science for comparing properties of
objects is to choose a related fundamental property of the same kind and set up
a relative scale on that basis.
Introduction of reduced variable. Divide actual variable by corresponding critical constant.
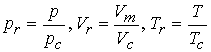
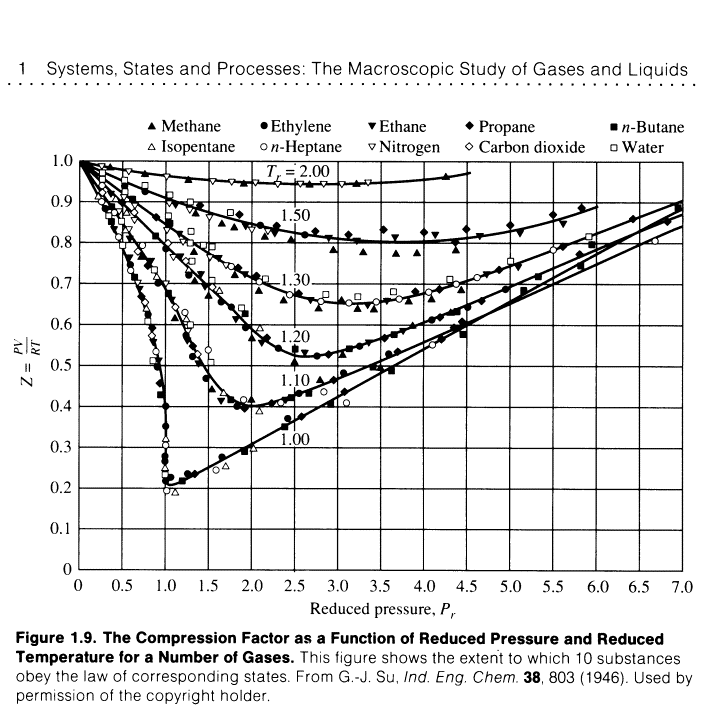
Van der waals hoped that that gases at the same reduced volume
and reduced temperature would give the same reduced pressure.
A great success. This
observation is called the principle of
corresponding states. Works well for spherical molecules.
If we express the van der Waals
equation in terms of reduced
variables and the constants a & b in terms of critical
constants,
the van der Waals equation in reduced variable form is:
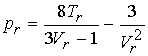
The coefficients a & b, unique to each gas, have
disappeared. Figure 1.26 on slide 10 is
a plot of reduced variable isotherms.
The same curves are obtained for any gas. van der Waals equation is compatible with the principle of
corresponding states.
Demonstrates that attractive and repulsive forces can each be
approximately accounted for with a single parameter each.
Chapter 2 First Law: The Concepts
Thermodynamics is a branch of science concerned with the
transformation of Energy. Four
laws: Zeroth Law, First Law, Second Law, & Third Law.
System º Object of interest ( part of the
universe we are interested in)
Surroundings º the rest of the universe, where we make
measurements, separated from system by a boundary.
Open System º Boundary allows transfer of heat and
matter between system and surroundings.
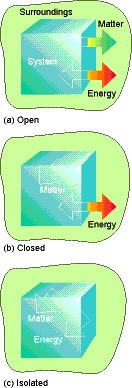
Closed System º Boundary allows transfer of energy but not
matter

Isolated System º
Boundary
does not permit transfer of energy or matter.
Fig. 2.1 pg 46
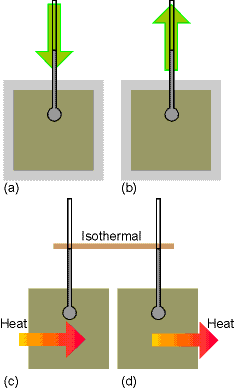
Work - the transfer of energy in a system in a manner equivalent
to raising a weight in the surroundings.
The symbol w stands for work done on the system and represents a
contribution to the internal energy of the system, brought about by the
equivalent of lowering a weight in the surroundings.
Energy - The energy, E, of a system is its capacity to due
work. The energy of a composite system
is the sum of all the kinetic and potential energies of all the particles in
the system.
Heat - description of a process rather than the name of a
form of energy. Energy is transferred
as heat between a system and surroundings if the transfer of energy occurs as a
result of a temperature difference between them. The quantity of energy
transferred is denoted q.
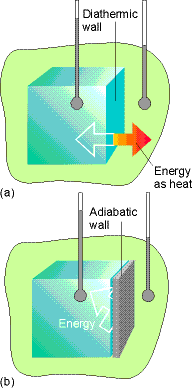

Fig. 2.2 pg 46 (an insulated system)

Molecular interpretation: Heat corresponds to the transfer of
energy that makes use of the energy of disorderly motion in the
surroundings, or which results in the stimulation of disorderly motion in the
surroundings. Distinguished from work
which makes use of ordered motion in the surroundings. Work results from collective uniform
molecular motion rather than random motion
Thermal motion - is random chaotic molecular motion, and
heat is the transfer of energy that makes use of this chaotic molecular motion.
Heat, q Work,
w
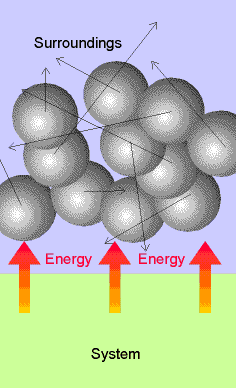
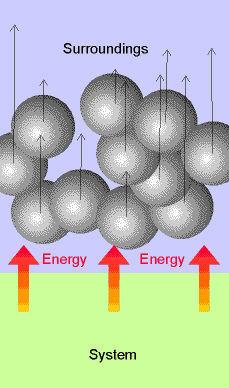


Fig.
2.3 & 2.5 pg 47
The First Law: the internal energy, U, of a system
is the total energy of all of its components.
It’s the total kinetic and potential energy of the system.
![]()
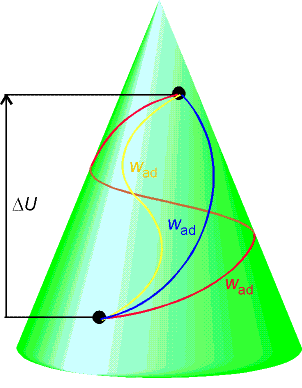
where wad
= adiabatic work (no heat transfer)
U is a state function.
A state function is a thermodynamic property that depends only on
the current state of the system and is independent of previous history (e.g. U
and entropy, S).
Example:
1. 2H2O(l) à 2H2O(g)
à 2H2(g) + O2(g)
2. 2H2O(l) à 2H2(g) + O2(g)
The two reaction mechanisms have the same initial and final
states, so they must have the same DU, change in internal energy.
The differentials of state functions are exact (their
integrals between two specified states is independent of path). It follows that the integral of a state
function around a closed path (cycle) is zero.
The difference in internal energy between two specified states is
equal to the work, wad needed to take the system from one state to the other along
an adiabatic path.
Molecular interpretation:
As the temperature of the system is raised, the internal energy
increases as the various modes of motion (translational, rotational,
vibrational) become more excited.
The first law represents a combination of the statements of the conservation of energy and the equivalence of heat and work as modes of transferring energy between a system and surroundings

Mathematical statement of first law:
DU = q + w heat + work
w>0, q>0 when energy is transferred to the system
w<0,q<0 when energy to transferred out of the system
Internal energy, heat, and work are all measured in the same
units, the joule (J).
The internal energy of an isolated system is constant (dU = 0).
Perpetual motion, generation of work without consumption of energy
is impossible.