In order to determine the locations of objects on the surface of the earth, we need to develop ways to measure it.  In order to measure the earth, we need to know its shape and size.  After many years of observation, we now have three pretty good approximations of the geometric properties of the earth.  They are the sphere, ellipsoid, and geoid.  Different models are used for different cartographic usages.

There are ellipsoids used for global mapping and positioning.  The earth, however, is an uneven object.  It is important to note that a single ellipsoid does lead to the best fit for every part of the world.  For that reason, many countries have established their own ellipsoids.

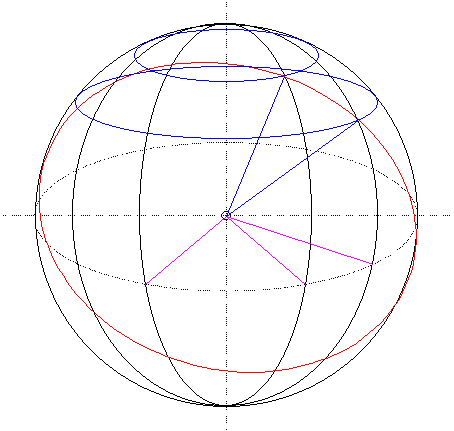
After we define the shape and size of the earth, a coordinate system is developed to locate each points on the surface of the earth.  That is the geographic coordinate system, which is formed by meridians and parallels and is measured for the north-south direction as latitude, and for the east-west direction as longitude.  Any point on the earth can be referenced by a pair of latitude and longitude.

Both latitude and longitude are angular distances.  For latitude, the measure starts at the equator and is ranged from -90 degree to +90 degree, or 90S to 90N.  For longitude, the origin is the meridian at Greenwich, UK, and is ranged from -180 degree to +180 degree, 180W to 180E.

When the earth is modeled as an sphere, the length of one degree latitude remains constant from the equator towards the pole while the length of one degree longitude decreases.  On an ellipsoid, the length of one degree longitude decreases towards the poles; the length of one degree latitude increases towards the poles.

The network of meridians and parallels in the geographic coordinate system is referred to as the graticule.  Unlike on the Cartesian coordinate system (plane coordinate system), the graticule, a spherical system, has its unique geometric properties.

• The shortest distance between two points on the earth surface is the length of the arc on the great circle. It is called the great circle distance and can be calculated based on the latitudes and longitudes of the two points.
• Direction on the earth surface can be defined in three different ways: geographic north or true north, magnetic north, and grid north.  Between two points, the true azimuth is defined at the starting point as the clockwise angle the arc of the great circle makes with the local meridian.  Except for traveling along the meridians or the parallels, the direction between two points changes constantly along the great circle.
• The true azimuth between two points on the earth can be calculated based on their geographic coordinates.  The true azimuth may be different depending on which point is considered to be the starting point.
• The line of constant direction is called the loxodrome or rhumb line.
• The significance of the area property of the graticule cannot be fully understood without putting it in the context of projection.  For example, if a projection forces the meridians to be equally spaced, such as the case in the Mercator projection, the areas would be greatly exaggerated towards higher latitudes.

Geodetic position determination

Geodetic positions can be determined through observations.  For example, geodetic latitude can be determined by measuring the angle between the local horizon and the Polaris.  Geodetic longitude has an artificial origin (Greenwich).  Because the earth is basically a sphere that completes one revolution in 24 hours, it is possible to determine the longitude through the difference at noon time (when the Sun reaches its highest altitude) from the Greenwich Mean Time, i.e., the time at the prime meridian.

It would not be terribly convenient if we always have to rely on the observation of the Polaris and the Sun, as well as accurate time information.  To accommodate everyday needs for position determination, control networks are established throughout the world.  These control networks serve as reference points for determining positions of other locations.  There are control networks for horizontal positions and there are those for vertical positions.  One of the key mathematical principles behind the working of these control networks is triangulation.

Triangulation includes a set of mathematical rules that determines the relations between the angles and the sides of triangles.  According to these rules, one can determine the distances and the horizontal positions of the unknown point if the length of the baseline and the coordinates of its end points, as well as  the angles with the sight lines are known.  Extending the baselines forms the horizontal control networks that cover an entire region.

Since the establishment of the baseline must make reference to a particular ellipsoid, the resulting horizontal control network is always tied to the particular ellipsoid.  The North American Datum 1927, or NAD27, for example, is based on the Clarke 1866 ellipsoid.

Vertical control networks are formed by level lines whose elevations at the endpoints are recorded.  The network starts at the point of mean sea level, extending to another datum point to form the first level line.  Subsequent level lines are established through various leveling techniques.  Trigonometric leveling is one of the popular method.  The vertical control network and horizontal control network do not necessary coincide with each other.

Control networks are referred to as datum.  We can therefore have horizontal datum and vertical datum.  For most cartographic projects, horizontal datum is more relevant than vertical datum.

One important aspect on the control networks is accuracy.  Different applications require different level of accuracy.  The greater the accuracy of the network, the more expensive to develop and to maintain.

GPS

Global Positioning System is a great leap forward in geodetic position determination.  With GPS, both horizontal and vertical positions, as well as velocity of movement, can be determined in real time.

• Satellite ranging.  By measuring the distances to three visible satellites whose positions are accurately defined, the three dimensional positions of an object can be determined.
• Distance measurement to the satellites is made possible by the atomic clock on board the satellites and the radio signals that carry the psudo-random code.  The fourth satellite guarantees a solution of position and makes it possible to use inexpensive clocks on the receiver.
• There are many factors influencing the accuracy of GPS.
• Accuracy can be improved dramatically through a technique called Differential GPS.
• GPS is widely available and is gradually replacing traditional methods of geodetic surveying.  However, accurate GPS still requires ground references.