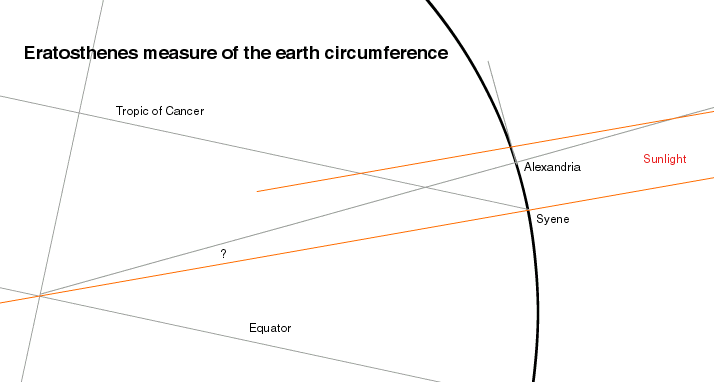
Since the angle of the sunlight at noon at Alexandria on the summer solstice is 82^48', the angle between the vertical line through Alexandria and the sunlight at Syene (which lit the bottom of the well) can be caculated as 90 - 82^48" = 7^12'.
Assuming the earth is a perfect sphere, Eratosthenes measured the circumference of the earth in a way illustrated by the graph below:

Since the angle of the sunlight at noon at Alexandria on the summer
solstice is 82^48', the angle between the vertical line through Alexandria
and the sunlight at Syene (which lit the bottom of the well) can be caculated
as 90 - 82^48" = 7^12'.
7^12" therefore is how far it is between Alexandria and Syene. Since the earth is assumed to be a sphere, the total arc length should be always 360 degrees. If you divide 7 degrees and 12 minutes by 360 degrees, or 7.2/360, the result is 0.02, or 1/50.
Now if the actual distance between the two locations is known, then we can figure out the circumference of the earth. The distance Eratosthenes found was about 925 km. Multiply 925 by 50, the result is 46250 km, which is Eratoshenes' measurement of the earth circumference.
Note:
When perform calculations for angular measurements, the best way is to convert them to decimal. Below is the formula to use:
Decimal degrees = Degrees + minutes/60 + Seconds/3600
References
Summer
solstics, by NASA